About that Wordle Thing

So this is going to be a tale of me finally winning a bet with my son, in the context of a deep, no-spoilers (unless you want them) analysis of Wordle as a data analysis problem. But let me repeat, I won a bet with my son!

Presumably if you’re interested enough to read this, you know about Wordle. If you don’t, hit that link and give it a try before reading, because pretty much nothing here is going to make sense if you don’t know what Wordle is! But this post is aimed at people who know about Wordle, who have tried to solve it, and want to know how good they are at it.

So like so many of us, I’m quite enjoying the game, and I came up with an approach to solve it that seemed pretty good. But I started to wonder how good my approach measured against the ideal. My son Aaron is pretty smart, at least when compared to a typical six year old. And I’m lazy, so I decided to get him to do the work for me.  Here’s how that worked out.

Note that bunches of this post will be interesting probably exclusively to computer scientist types, but if you want to drive people away from you at parties, this will give you plenty of ideas of how. Note also that there will be spoilers here, but they don’t start until about halfway through. I’ll put a big “spoiler warning” before I start talking about anything that would help you actually think about game strategies. However, at the end I’m going to probably spoil it entirely, giving you a strategy that is reasonably close to optimal.

Summary

1. The idealized, mathematical minimum (with all kinds of erroneous assumptions) is 2.27 guesses. It’s not mathematically possible to do better than that. It’s not actually possible to do that, either, though.
2. The actual minimum average guesses, for a pretty decent solver, is about 3.8 guesses.
3. If you cheat, like my son did to start (not really, relax, I’m just making fun of him, because he’s a cheating cheater who cheats) but my point is that if you cheat like my son did (and most of the solutions I’ve seen on the net also do), the effective minimum is an average of 3.49 guesses.
4. My simple, practical approach results in about 3.95 guesses. Not bad!

How I Nerd-sniped My Son

So a couple weeks ago Nate Silver posted this tweet:

The answer for puzzle 205 was “query”, which makes the last six guesses… amusing. I mean, what the hell letter did he think follows “Q”? I want to see those words!

And that was my in. I shared that with Aaron, and challenged him to play. It took him five guesses. I told him “I solved it in three. I’d tell you how I got the answer so quickly but that’s half the fun,” and he responded:

Victory! The hook is in.

For the record, he didn’t crush me.

Some Theory and Some Math: 2.27 guesses

To estimate the mathematical minimum, we first did some research and some thinking. Now, full confession: pretty much anything smart that happens from here on comes out of my son’s brain. I’m pretty much just the stenographer for this journey.

Webster’s Dictionary suggests there are around 470,000 words in the English language. The Oxford English dictionary cites 200k total words. Of course that is words defined  so “drive” and “drove” (along with drives and driving) would all appear as one word; the total number is far higher. However, according to The Free Dictionary, there are 158,390 five-letter words in the English language. So we will accept that as our search space – we’re going to pretend we want to find a word from a list containing about 150,000 words, in six guesses.

At each step, each guess gives us a clue corresponding to each letter position. Specifically, we have a clue consisting of five pieces of information, each of which can be in one of three states: correct letter in the correct position; correct letter in the wrong position; incorrect letter. This means that each clue represents one of 3^5=243 possible states. (The computer scientists reading this are about to start talking about trinary, but I won’t do that.) (I mean, I just did? Kinda? But I won’t any more.) Ok, but said another way, this means that every guess occupies a position in a five digit trinary number system. (Dammit!)

Now, the goal is to maximize information gain: to find the single word that Wordle is thinking of as quickly as possible. Mathematically, this means that we want to eliminate as many words as possible with each guess. So, now, we’re about to make a massive assumption: let’s assume, just for fun, that the remaining words (all the words, to start) are sorted into buckets of exactly equal size, each bucket identified by a unique clue. There will be 243 such buckets.

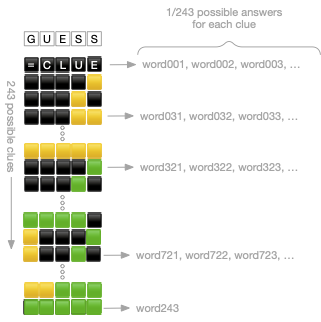
This means that if English is astonishingly well distributed across the clues – as my son put it, “assuming spherical cows” – each guess will eliminate all of the words except the 1/243 of them that are in a specific clue bucket. So after one guess, we’ll have 1,108 words left; after two guesses, five words; our next guess will eliminate all the buckets but one, and then we’ll guess it. That is, the ideal theoretical minimum to solve Wordle takes n guesses, where 158,390 = 243^n. Wolfram Alpha says this is 2.18 guesses to reduce it to one bucket, with one additional guess to pick the actual word (the base case, where n is zero). So this suggests that the mathematical best we can do is 3.18 guesses.

On “Cheating” – Pure, Fair, and Cheaty approaches

But it turns out, we know a little more about Wordle: the dictionaries Wordle uses are present in the source code. There are two of them, the “guessable” dictionary that defines all valid guesses, and the “answers” dictionary that the app uses to select the solution (the word the app is thinking of). The one that defines all legitimate guesses is reasonably large, including 12,972 words, but nowhere close to the 150,000 we started with. On the other hand, the answer dictionary is much, much smaller, including only 2,315 words.

So now we were faced with a conundrum. What information are we allowed to use when we’re trying to solve this puzzle? Should we use a dictionary with the full 150,000 words? Or do we want to be psychic and use the solution dictionary directly? Since we are ultimately trying to decide about how good we are at Wordle, and guessing a word that isn’t in the guessable dictionary doesn’t give us a clue or cost us a turn, we decided that we could use that dictionary and not be cheating. But to test our solutions, we came to an impasse. I’m pretty goal focused, so I suggested it would be reasonable to iterate across all possible answers and see how our solver does with them; my son is a theorist, and said that it would only be “pure” if we tested against the full answer dictionary as well.

He also pointed out that if we did use the answer dictionary to test our solver, and used an iterative solution, he could eventually train a model that would eliminate words that weren’t guessable – in effect discovering the answer dictionary.

So we ended up with three versions. The “pure” version makes my son happy, and uses only the answer dictionary, both to generate the solver and to test it. As he likes to point out, that solver is prepared for a change to the underlying answer dictionary. The “fair” version is the one I wanted, that tells us how a human could do against the real answer dictionary, but is precluded from using that knowledge in its solution. The “cheaty” version uses only the answer dictionary, including to generate the solver.

It turns out that the mathematical difference between fair and cheaty is about a third of a guess: the fair approach should take 2.7 guesses, and cheaty should take 2.4 guesses. In practice the difference is more significant: the fair version takes 3.8 guesses for our best solver, while the cheaty version only 3.49 (and the pure version, which assumes that any guessable word could be the answer, takes an average of 4.12 guesses).

But now we have a mathematical minimum: in theory, limiting ourselves to the dictionary of guessable words, we should be able to guess in 2.7 guesses.

Wait but What Now?

So the problem with this is that it completely fails the smell test. If on average we can guess in 2.7, then there must be a magical word that allows us to guess correctly immediately after (two guesses total) about a third of the time. That is obviously wrong! Well, as it turns out, cows aren’t spherical, and English isn’t well behaved. The words aren’t going to be well distributed.

So what is the actual minimum? Computing that required writing the solver my son promised.

Not only did he not crush me… now he totally owes me beer! This was the best nerd snipe ever. If only he was mature enough to drink with me.

The Solver

The basic approach for a solver is pretty straightforward.We know that every guess will produce a clue, and as described above that clue is one of 243 possible values. So we start by creating a map keyed by the clue value (really an array, since we know there are exactly 243 possible clue values), each containing an empty set – let’s call this the “clue space” for a guess, and the set of words associated with each clue the “clue bucket.” So for each guess, we want to populate the clue space, filling all the clue buckets. This is pretty straightforward: we iterate across all of the guessable words; for each guess, iterate across all possible answers; for each guess/answer pair, generate the appropriate clue; then add that answer into the “clue space” for the generated clue. When we’re done, for each guessable word we now have a “clue map” that has collected all the words for each clue into a bucket. So, in ruby-like pseudo-code:

choose_guess() {
  guesses.each { guess |
    clue_space = Map.new()

    answers.each { answer |
      clue = generate_clue(guess, answer)
      clue_space[clue].append(answer)
    }

    current_score = generate_score(clue_space)

    if (current_score > best_score) {
      best_score = current_score
      best_guess = guess
    }
  }

  return best_guess
}

What’s left is the interesting part: how to generate the score for the clue space associated with each guessable word. Scoring a word means iterating across the 243 possible clues, computing a partial score based on the contents of the bucket, and then computing an aggregate for all the clues. Per above, the ideal word will generate 243 sets of exactly the same size – which we know isn’t possible, but we dream, we dream. So the score should be better the more balanced clue space is – that is, the closer in size the contents of the clue buckets are.

Let’s Get Intuitive

To clarify what this means, consider a simplified world where we have 200 total words, and only 100 possible clues. Now let’s consider two competing guesses. The word “woot!” results in a nicely balanced collection of 100 buckets each containing exactly two words; meanwhile the word “stink” is completely unbalanced, yielding 99 buckets containing only one word, and a single bucket with 101 words.

Our balanced “woot!” means that after the first round we’ll have found a clue that eliminates all the words but the two in its clue bucket. Then, since we have only two words left, we will either guess in the next round or the one after that; so it’ll be two rounds half the time and three the other half. Thus “woot!” gives us an expected average of 2.5 rounds, and it’ll never take more than three. (Remember, we’re working through an itty-bitty sample; the real solver has many more words, and many more buckets, which is why even in theory it will take more guesses.)

“stink” is harder to analyze. In each round “stink” gives us basically a 50% shot guessing the word and a 50% chance of needing at least another round, repeating with half of the words remaining. From an analytic perspective, it’s useful to think about this not as how many we have, but instead how many we eliminate: guessing the word eliminates all of them, while not guessing it eliminates half. So half the time we eliminate all of them, and half the time we eliminate half of them. This may be counterintuitive to a non-statistician, but with that in mind it means that on average we’re eliminating 75% of the words in each round (50% * 1  +  50% * 0.5); this means that we can expect n rounds to guess, where 200 = 4^n solve for n, which means this wildly unbalanced world will have us take 3.8 rounds (and again, this is an itty-bitty sample yet it would drastically underperform the ideal).

But wait! It gets even more stinky! If we think instead about how well we might be able to do, this approach means we will guess immediately half the time (lookin’ good); it will take two guesses a quarter of the time, three guesses an eighth of the time, and so on. From this perspective we’re doing a binary search, which means that worst case we’ll have to keep eliminating half of the population until we get down to exactly one left. Since there are 200 words, we know that it might take as many as eight guesses (log2(200) = 7.6) – and Wordle only gives us six! So 1/256 of the words will take eight guesses, and 2/256 will take seven, meaning that for 3/256 of the words, or 12% of the time, we will fail entirely! And, finally, again, recall this is an itty-bitty example; there are actually 2,315 answers, and log2(2315) = 11.2 – so the binary search approach could take as many as 12 guesses!

Stinky indeed. So we want to be as close to “woot!” as possible.

Scoring:  Maximum Contribution

Even with all that theory behind us, the approach my son took remains harder to describe than to implement. Given a guess, a specific possible clue for that guess, and the associated bucket of answers that would result in that clue, there are two interesting properties to consider:

1. p(clue): What are the odds we would get that specific clue?
2. v(clue): What would getting that clue do for us?

Given that we have equal probability of any guessable word being the answer, the odds of getting a clue is exactly proportional to the number of words in the bucket, out of the total guessable words. For example, again in our hypothetical 200 word universe, if we have one word in a bucket, the odds of getting that clue are 1/200; if we have 100 words in the bucket, the odds of getting the clue is 100/200. Then generally the probability of getting a clue is just p(clue) = bucket_size / available_words where bucket_size is the number of words in the set associated with that clue, and available_words is the total number of words that are still possible answers.

The question of the value of getting that clue is perhaps a bit tricksy. One way to think about it is that it would contribute some fractional amount towards a solution, proportional to the number of words in the bucket; then the value of a clue is just v(clue) = p(clue) * bucket_size. Putting those together, v(clue) = bucket_size^2 / available_words. Then the value of an answer is just the sum of v(clue) for all its clues.

To test the approach, we just add one more loop outside all of this, and iterate through all the answers and see how our solver does (well, that’s the fair approach; in the pure approach we would iterate through all the guessable words). This let Aaron determine that this solver will guess the Wordle in an average of 4.07 guesses. But, as I mentioned at the beginning, my less sophisticated approach had already reached an average of 3.95… and Aaron refused to believe I could beat his super-duper statistical algorithm. So he had more work to do.

The Final Strategies

Note that there is one important initial observation to be made here: when choosing the next word to guess, we want to consider all the remaining guessable words, not just the available words in the bucket, constrained by prior clues! If we use any available word for our guess, we get that average of 4.07 guesses. But if we instead limit ourselves to guessing only words that are possible answers, given the clues we’ve already gotten (that is, guessing from words in the clue bucket), we get far worse performance – an average 4.35 guesses (and worse, failing entirely 1.6% of the time) – even if we’re being cheaty (guessing from the 2k answers dictionary, rather than the 12k guessable dictionary).

That is a pretty big hint for how you might approach improving your Wordle play, if you hadn’t already thought of it: as you think about your second or third guess, it is often better to ignore the prior guesses and continue to seek letters, until you have enough that it is reasonable to think you can actually guess the word.

So What Words Should I Use?

At this point you may be looking to the solver to tell you what word to use first, because everyone knows that it’s important to use technology to solve problems instead of, you know, thinking about them. I have good and bad news: the good news is that the solver thinks that the word you should use is “ROATE,” if you’re being cheaty, and “LARES” if you don’t want to be all cheaty-like. However, the bad news is that using these starting words will not help you.

The reason knowing the “best” word doesn’t help much is that we need to consider what the solver does next. For the “fair” solver, using LARES as the first guess, the next guesses are highly dependent on the clue we get. The top 10 words it uses next are quite unpredictable, and only get us to 42% of the total words used! That is, to use this, you need to actually know the set of associated words in the clue bucket. So trying to use LARES won’t actually help you play Wordle.

tondi	7.96%
tonic	6.41%
knout	5.84%
point	4.56%
conia	3.49%
minty	3.08%
donut	2.86%
piony	2.84%
tunic	2.61%
stoai	2.43%

More Intuition

Let’s take a look at an example of what the solver actually does. Note: for simplicity, I’m going to call the three states of a clue “Great!” “yummy,” and “-bogus,” which I choose because they start with a letter corresponding to the colored green, yellow, black squares Wordle displays. This means can represent a clue using the letter shorthand “G”, “y”, and, “-” respectively.

So as an example I beat the cheaty solver on the 1/11 puzzle; I got it in three, but the solver took four! Clearly I’m superior! But it turns out it was just random luck. The solver chose:

1. ROATE (y----)
2. SCULK (----G)
3. BRINK (-GGGG) [oh so close!]
4. DRINK (GGGGG)

After the second guess the clues have told us that the word ends in K, and has an R in it somewhere after the first letter. Doesn’t help me much, to be honest, but at this point the solver was down to exactly two words, and basically picked one at random. It was as likely to guess right as wrong, but missed this one and needed that extra guess.  This may help give a bit more instinctive understanding of why the average ends up being more than three: a fair number of guesses will quickly discriminate down to words with 2-3 variants on a common stem, and then it’s random luck between them.

Can We Betterify the Solver Still More?

Consider how the solver approached the 1/19 puzzle:

1. LARES (-----)
2. TONIC (yGyy-)
3. NOINT (-GGGG)
4. POINT (GGGGG)

Ok, so after the second guess, again our solver was down to only two words. But in this case our solver was all like, hm, it’s either NOINT or POINT, and goddam am I definitely feeling all the love for NOINT! Which, speaking from the perspective of not-the-solver, is a word I’ve never heard before and isn’t defined in many dictionaries. So, maybe not what a person would do.

So then my son and I had a long debate about what was an acceptable optimization, because – again – using the solution dictionary at all as input to the solver seemed like cheating. We ultimately agreed that using frequency information available on the web was legit (which was a relief to me, since – well, see below), so he then just sorted the questions dictionary by word frequency in English (using the frequency data available from Kaggle). The solver would now break ties in favor of the more common word. This improved the performance notably; the fair version now guessed in 3.8, and the cheaty version in 3.49. Congratulations, Aaron, you’ve beaten me!

My Approach

So as a reminder, my approach resulted in an computed average of 3.95 guesses, which so far has worked out in practice (the first couple “five step” guesses in my histogram below were before I came up with the approach I’m about to describe). What I did was straightforward. The letter frequency in English is quite well known. All I did was list the most frequent letters and then construct a set of guesses that would use as many of them as possible.

The most frequent letters in English, as computed by Samuel Morse when he was working on the eponymous code, are: ETAION SHRDLU CMFWYG PBVKQJ XZ (but A, I, N, O, and S are equally frequent.)

So from these I constructed three words:

TREAD, LIONS, and CHUMP.

To play, I just guess TREAD and if I don’t get enough letters to guess (which I haven’t yet) I guess LIONS.

Now, going back to the 1/11 puzzle, my game was:

1. TREAD (-G–y)
2. LIONS (-y-G-)
3. DRINK (GGGGG)

After the second guess, I knew that the word was -R-N- with both a D and an I in there, so “DRINK” was obvious. But if the word had in fact been BRINK – which is equally likely, in the grand scheme of things – I would have struggled a lot more.

But I also did really nicely on the 1/19 puzzle:

1. TREAD (y—-)
2. LIONS (-yyG-)
3. POINT (GGGGG)

With this approach, about a third of the time I can guess in three; then if I still don’t have enough letters, I guess CHUMP, which means I’ve examined just over half of the most common letters in English. I’ve almost always been able to get it in three or four. But it turns out this approach is vulnerable to doubled letters, especially uncommon doubled letters. I don’t remember what I did after the third guess, but the 1/13 puzzle almost got me:

1. TREAD (–yy-)
2. LIONS (—–)
3. CHUMP (—-)
4.
5.
6. ABBEY (GGGGG)

So there you have it. TREAD, LIONS, CHUMP, worry about doubles. Win!

 

But Wait! There’s More!

Did you know that Wordle Has a Hard Mode? In the comment section below my friend Geoff told me that there is, which is something of which I was completely unaware. So, naturally, we did some analysis of that too. Click that link to see yet more Wordle analysis! Of course, if you click that link you probably need to admit to yourself you have a problem. Because… really?

Conclusion

So I’ve seen a lot of twitter backlash about this game, but I think it’s quietly elegant and completely deserves the attention it’s been getting. Josh Wardle, the game’s creator, fully deserves the accolades.

I hope anybody who has gotten this far enjoyed the analysis. It was a fun conversation getting here.

But most importantly, of course, my son owes me a beer. And we both need to get out more. COVID is stupid.